$\star$ 우선 설명하기에 앞서, convex/non-convex가 무엇인지, 전체적인 deep learning내에서의 수식 등에 대해서는 생략하도록 하겠습니다. 다른 블로그들에 워낙 잘 나와있어서 굳이? 일 것 같습니다. 다만, 저는 여기서 “왜?”, 또는 “어떻게?”에 대해 좀 더 초점을 맞춰 작성해보도록 하겠습니다. 특히, 수식전개에 좀 더 초점을 맞춰보도록 하겠습니다!! ![]()
Why Convex Optimization?
대부분 저희가 실제로 풀어야하는 문제들은 non-convex 형태입니다. 그런데 이런 non-convex한 function를 해결하기 위해서는 더욱 정교한 approximation과 증명이 필요로 합니다. 이렇게 됐을 때, cost도 너무 커질뿐만 아니라 비효율적일 수 있습니다. 그런데 만약 우리가 가정할 수 있는 범위 내에서 해당 function이 convex 하다는 것을 가정하고 푼다면 효율적으로 해결할 수 있을 것 입니다. 즉, 만약 임의의 function $f$가 convex 하다고 가정한다면 $f$에 대한 local minima가 곧 global minima이기 때문에, local minima만 찾으면 되기 때문에 해결해야하는 task가 비교적 매우 쉬워집니다. 그렇다면 간단한 예시들을 통해서 한번 살펴보도록 하겠습니다.
아래 Taxonomy는 optimization 시 분류하는 기준을 나타냅니다.
$\star$ Taxonomy:
- Zeroth Order: Only value of Function
- $1^{st}$ Order: Derviation (GD/ SGD/ mini-batch GD 등)
- $2^{nd}$ Order: Hessians (Newton Methods 등)
Example: Gradient Descent
Deep Learning field에서 최적의 해를 찾기 위해 제일 기본 method 중 하나가 Gradient Descent(이하, GD)입니다. 사실 요즘은 GD가 아니라 대부분 다른 optimization 기법(e.g., SGD, Adam 등)을 사용하지만, GD에서 대해서 최적화적인 관점에서 어떻게 수렴하는지를 이해하면 나머지 기법들도 순차적으로 이해할 수 있을 것 같습니다.
그렇다면 이제 GD에 대해 optimization이 어떻게 이루어지는지, 그리고 assumption에 따라 어떻게 optimization의 수렴형태가 변화하는지를 살펴보도록 하겠습니다. (여기서의 모든 assumption은 convex를 기준으로 합니다)
Problem Formulation 1
(Assumption: $L$-Lipschitz)
들어가기에 앞서 간략하게 optimization 설정을 보통 다음과 같이 합니다:
\[\min\limits_{x \in \mathbb{R}^d} f(x)\]where $f$ is differentiable convex function.
그리고 GD는 모두가 알다시피 iterative algorithm이므로 다음과 같이 적을 수 있습니다:
\[x_{k+1} = x_k -\gamma \nabla f(x_k)\] where $\gamma > 0 $ is the step size, a.k.a learning rate
그렇다면 optimal solution을 찾기 위해 위의 내용을 계속해서 반복할 것입니다. 만약 학습이 발산하지 않고 진행된다고 가정한다면, 좋은 optimization algorithm은 얼마나 빨리 optimal solution을 찾냐의 싸움입니다. 그럼 이걸 어떻게 찾냐?라고 했을 때, 최종 step $T$에 대해서 upper bound 설정을 통해 찾을 수 있습니다. 즉, 학습이 최종적으로 진행됐을 때
Theorem 1: Let $f$ be convex and $L$-Lipschitz continuous. Then gradient descent with $\gamma = \frac{\mid\mid x_1 - x^\star\mid\mid}{L\sqrt{T}}$ satisfies:
\[f \left ( \frac{1}{T} \sum_{k=1}^T x_k \right) - f(x^{\star}) \leq \frac{|| x_1 - x^\star || L}{\sqrt{T}} \Rightarrow \mathcal{O}(\frac{1}{\sqrt{T}})\]Proof:
우선 문제를 해결하기 위해선 convex sets에 대해서 projection 하는 방법으로 해결할 수 있습니다. 즉 다음 그림과 같은 inequality를 만족시켜 나가는 형태로 전개할 수 있습니다 (글을 발로 적었음을 미리 말씀드립니다..ㅠㅠ)

즉, convex sets에 대해서 projection했을 때, projection 위치 $\pi_c (z)$에 대한 $x$와 $z$의 inner product는 항상 음수(둔각)가 나오고 이를 피타고라스 식을 활용하면 $\mid\mid \pi_c (z) - x\mid\mid \leq \mid\mid z - x \mid\mid$ 의 inequality가 성립합니다. 또한 나중에 proof 전개 시 피타고라스 정리를 다음과 같이 활용할 예정입니다: $\mathbf{\left<a,b\right> = \frac{1}{2}(\mid\mid a\mid\mid^2 + \mid\mid b\mid\mid ^2 -\mid\mid a-b\mid\mid ^2)}$)
그럼 위의 properties를 활용해서 proof를 전개해보겠습니다:
\[\begin{align} f(x_k) - f(x^\star) &\leq \; \;\left<\nabla f(x_k) \;, \; x_k - x^\star \right> \; \rightarrow \text{1st order convexity}\\ &= \; \left<-\frac{1}{\gamma}(x_k - x_{k+1}) \;,\; x_k - x^\star\right> \; \rightarrow \text{$x_{k+1} - x_k = - \gamma \nabla f(x_k)$ }\\ &= \frac{1}{2\gamma} \left[ \; \mid\mid x_k - x_{k+1}\mid\mid ^2 + \mid\mid x_k - x^\star\mid\mid ^2 - \mid\mid (x_k - x_{k+1}) - (x_k - x^\star)\mid\mid ^2 \; \right] \rightarrow \; \text{pythagoras theorem}\\ &=\frac{1}{2\gamma} \left[ \; \mid\mid x_k - x^\star\mid\mid ^2 +\mid\mid \gamma \nabla f(x_k)\mid\mid ^2 - \mid\mid x_{k+1}- x^\star\mid\mid ^2 \; \right] \\ &= \frac{1}{2\gamma} \left[ \; \mid\mid x_k - x^\star\mid\mid ^2 - \mid\mid x_{k+1} - x^\star\mid\mid ^2 \right] + \frac{\gamma}{2} \mid\mid \nabla f(x_k)\mid\mid ^2 \end{align}\]여기서 $L$-Lipschitz Continuity 성질: 만약 $f$ 가 differentiable 하면 $\mid \nabla f (x) \mid \leq L$ 이다. $\rightarrow \frac{\gamma}{2} \mid\mid \nabla f(x_k)\mid\mid ^2 \leq \frac{\gamma L^2}{2}$ 을 활용하면 다음과 같이 bound를 설정할 수 있습니다.
\[\begin{align} \frac{1}{2\gamma} \bigg [ \; \mid\mid x_k - x^\star\mid\mid ^2 - \mid\mid x_{k+1} - x^\star\mid\mid ^2 \bigg] + \frac{\gamma}{2} \mid\mid \nabla f(x_k)\mid\mid ^2 \\ \leq \frac{1}{2\gamma} \bigg [ \; \mid\mid x_k - x^\star\mid\mid ^2 - \mid\mid x_{k+1} - x^\star\mid\mid ^2 \bigg] + \frac{\gamma}{2} L^2 \end{align}\]그럼 이제 순차적으로 $k$ 값을 대입해서 식을 전개해보겠습니다!!
\[\begin{align} f(x_1) - f(x^\star) &\leq \frac{1}{2\gamma} \bigg [ \; \mid\mid x_1 - x^\star\mid\mid ^2 - \mid\mid x_{2} - x^\star\mid\mid ^2 \bigg] + \frac{\gamma L^2}{2} \\ f(x_2) - f(x^\star) &\leq \frac{1}{2\gamma} \bigg [ \; \mid\mid x_2 - x^\star\mid\mid ^2 - \mid\mid x_{3} - x^\star\mid\mid ^2 \bigg] + \frac{\gamma L^2}{2} \\ &\;\;\vdots \\ f(x_k) - f(x^\star) &\leq \frac{1}{2\gamma} \bigg [ \; \mid\mid x_k - x^\star\mid\mid ^2 - \mid\mid x_{k+1} - x^\star\mid\mid ^2 \bigg] + \frac{\gamma L^2}{2} \\ &\;\;\vdots \\ \end{align}\]Inequality의 양쪽 hand side에 대해서 평균을 내면 다음과 같습니다:
\[\frac{1}{T} \sum_{k=1}^T \bigg[ f(x_k) - f(x^\star)\bigg] \leq \frac{1}{T*2\gamma} \bigg[ ||x_1 - x^\star||^2 - ||x_{T+1} - x^\star||^2 \bigg] + \frac{\gamma L^2}{2}\]여기서 $\mid\mid x_{T+1} - x^\star\mid\mid ^2$ 는 앞에 $-$가 붙어있으므로 이 term은 항상 음수가 됩니다. 따라서 이를 그냥 소거하여 upper bound를 추가로 설정해줄 수 있습니다.
\[\Rightarrow \frac{1}{T*2\gamma} \left[ || x_1 - x^\star || ^2 - || x_{T+1} - x^\star || ^2 \right] \leq \frac{1}{T*2\gamma} \cdot || x_1 - x^\star || ^2\]그리고 나서, *Jensen’s Inequality를 활용하여 $f(\frac{1}{T} \sum_{k=1}^Tx_k) \leq \frac{1}{T} \sum_{k=1}^Tf(x_k)$ 로 나타낼 수 있습니다. (이미 $f$ 는 convex하다고 가정하였기 때문에)
*Jensen’s Inequality: 만약 $f$ 가 convex 하면, $f(\mathbb{E}[x])\leq \mathbb{E}[f(x)]$ 을 만족한다.
이에 따라서 수식을 전개하면 다음과 같습니다:
\[\begin{align} f(\frac{1}{T} \sum_{k=1}^Tx_k) - f(x^\star) &\leq \frac{1}{T} \sum_{k=1}^Tf(x_k) - f(x^\star) \leq \frac{\mid\mid x_1 - x^\star\mid\mid ^2}{2\gamma T} + \frac{\gamma L^2}{2} \\ \Rightarrow f(\frac{1}{T} \sum_{k=1}^Tx_k) - f(x^\star) &\leq \frac{\mid\mid x_1 - x^\star\mid\mid ^2}{2\gamma T} + \frac{\gamma L^2}{2} \\ \end{align}\]마지막으로 step size $\gamma = \frac{\mid\mid x_1 - x^\star\mid\mid}{L\sqrt{T}}$ 를 대입하면
\[\begin{align} f(\frac{1}{T} \sum_{k=1}^Tx_k) - f(x^\star) &\leq \frac{|| x_1 - x^\star|| ^2}{2\gamma T} + \frac{\gamma L^2}{2} \\ &= \frac{L \sqrt{T}}{|| x_1 - x^\star|| } * \frac{|| x_1 - x^\star|| ^2}{2 T} + \frac{L^2|| x_1 - x^\star || }{2*L \sqrt{T}} \\ &= \frac{L\sqrt{T}(|| x_1 - x^\star || )}{2T} + \frac{L\sqrt{T}(|| x_1 - x^\star || )}{2T} \\ &= \frac{L || x_1 - x^\star|| }{\sqrt{T}} \end{align}\]이와 같이 전개했을 때 Theorem 과 동일하게 나오는 걸 볼 수 있습니다!! 이 말인 즉슨, $T$에 따라 convergence rate이 달라지는데 $f$가 convex 및 $L$-Lipschitz 하다고 가정했을 때, 그 속도는 $\mathcal{O}\left(\frac{1}{\sqrt{T}}\right)$에 수렴한다는 의미입니다!!
번외: Fixed Step Size vs. Adaptive Step Size
다른 textbook, 논문, 블로그 등을 보면 Gradient Descent를 증명할 때 fixed step size $\gamma = \frac{1}{L}$ 로 두고 derive를 하곤 합니다. 사실 이렇게 했을 때 수식적으로도 상당히 깔끔하고 convergence rate도 $\mathcal{O}(\frac{1}{T})$ 로 더 빠릅니다. 다만 이렇게 진행했을 때, constant한 value를 설정해야한다는 점, 그리고 수식전개를 할 때 fixed step size 면 bound RHS에 $\frac{1}{T}$ 의 관한 independent한 term이 생기게 되면서 정말 minimum으로 간다고 장담할 수 없게 될 수 있습니다 . 따라서 제가 전개한 방법은 convergence rate을 포기하더라도 실제 첫 input $x_1$ 과 optimal $x^\star$ 간의 차이와 거기에 iteration 횟수 $T$ 에 대해서 dependent하게 step size를 설정하여 조금 더 adaptive 한 step size를 만드는 것으로 이해하면 될 것 같습니다.
(Fixed Step Size에 대한 증명은 워낙 많이 나와있어서 생략하겠습니다)
이 후…
위와 같은 전개는 $f$ 를 convex 및 $L$-Lipchitz continuous하다는 가정을 하고 전개한 수식입니다. 만약 assumption이 더 강력해진다면 ($\beta$-smooth, $\alpha$-strongly convex 등 ) convergence rate이 달라지게 됩니다. 이후 posting은 assumption에 따른 convergence rate을 증명하는 것으로 진행하도록 하겠습니다.
마지막으로 GD에 대한 assumption에 따른 convergence rate 표를 소개하면서 마치겠습니다.
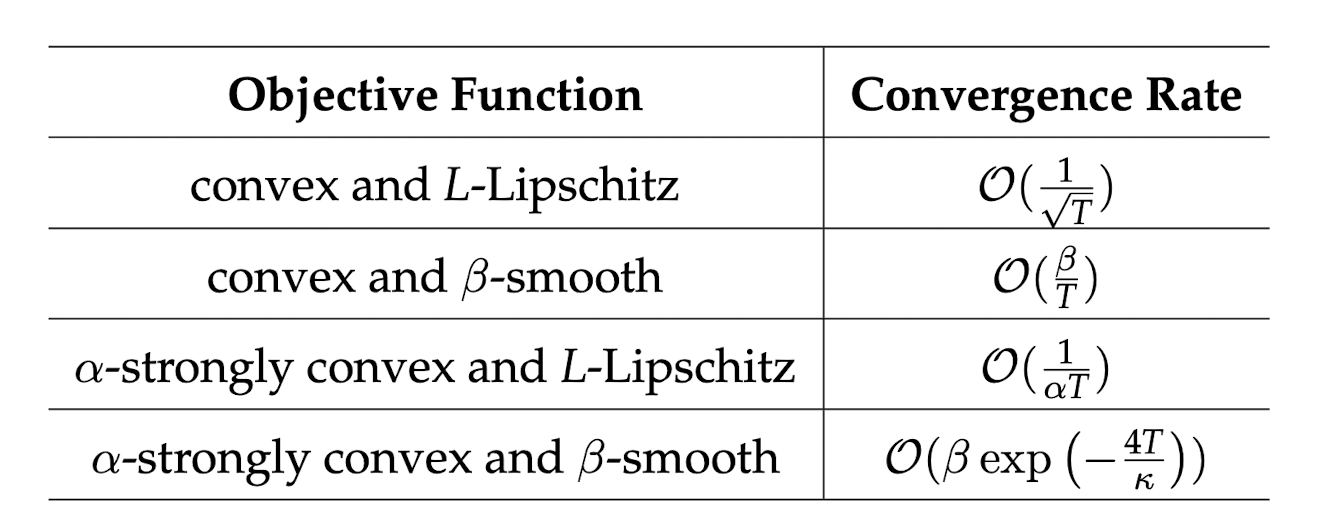
$*$읽어주셔서 매우 감사합니다!! 혹시나 글을 읽으시다가 틀린 부분이 있거나 조언해주실 부분이 있다면 언제든 의견 전달주시면 감사하겠습니다!! ![]()