Recap of Weight Decay (WD)
최근 model을 학습시킬 때, 대부분 Weight Decay (WD)를 사용하곤 합니다. WD를 사용했을 때 가져다주는 이점이 많은데, 대표적인 효과로는 overfitting 방지 입니다. 그렇다면 WD가 무엇이길래 overfitting을 방지할 수 있을까요?
대체적으로 Deep Learning을 처음 접할 때 WD를 다음과 같이 배울 것입니다:
\[\begin{equation} \mathcal{L}_{total}= \textcolor{red}{\underbrace{\frac{1}{n}\sum_{i=0}^n \ell(f(x_i;\theta), y_i)}_{\text{Loss Function }(\mathcal{L}(\theta))}} + \textcolor{blue}{\underbrace{\frac{\lambda}{2}||\theta||_2}_{\text{WD}}} \label{eq:weight_decay} \end{equation}\]즉, 위와 같이 Loss Function을 통해 학습을 할 때, 기존 도출된 loss에 더하여 model의 weight parameter의 norm 값도 같이 줄이는 방향으로 학습을 하게 됩니다. 이렇게 됐을 때, 직관적으로는 대부분의 weight parameter를 0 근처로 보내게 되면서 model의 complexity를 줄어들고, 이를 통해 overfitting을 방지하는 효과를 볼 수 있습니다.
하지만 여기서 WD의 역할을 조금 더 깊게 살펴볼 필요가 있습니다. 이유는 WD의 역할이 단순히 ‘Overfitting 방지’에만 국한되지 않기 때문입니다. 예를 들어 최근에는 LLM같은 매우 큰 model에도 WD는 필수로 적용하는데, 생각해보면 LLM은 매우 큰 datasets에서 1 epoch정도로 학습하기 때문에 굳이 overfitting을 고려할 필요가 없기 때문입니다. 그럼에도 불구하고 (오히려) 더 큰 WD ratio $\lambda$를 걸어 진행하곤 합니다.
따라서, 이번 글에서는 제가 생각하는 WD의 역할 및 그 의의에 대해 설명 해보도록 하겠습니다.
1) WD는 사실상 Prior Knowledge 분포이다!
딥러닝 분야에서 통계적 모델링을 할 때 흔히 사용하는 ‘대표적인 가정’이 하나 있습니다. 어떤 분포를 설정해야 할 때, 가장 다루기 쉬운 Gaussian Distribution을 따른다고 가정하는 것입니다. 이유는 단순합니다. 정규분포는 복잡한 파라미터 없이 오직 평균(Mean)과 분산(Variance)만 알면 분포 전체를 완벽하게 정의할 수 있기 때문입니다. 따라서 저도 본격적인 설명에 앞서, 다음과 같은 가정을 깔고 들어가겠습니다:
가정: Model weight parameters가 gaussian 분포를 따른다.
만약 위 가정이 성립되면 다음과 같이 statement를 도출할 수 있습니다:
WD는 weight가 gaussian prior를 가정한 Maximum A Posteriori (MAP) 추정이다.
그렇다면 이제 말이 무슨 뜻인지 천천히 살펴보도록 하겠습니다. 여기서는 딥러닝 학습을 optimization 관점으로 보는 것이 아닌, 최적의 해를 찾을 수 있는 probability의 관점으로 바라보겠습니다.)
(해당 내용은 PRML Chaper 3.3의 내용 및 여러 자료들을 취합해서 작성했습니다.)
MLE에서 MAP로의 개념 확장
보통 학습 시 Loss Function(e.g., MSE, CE)을 최소화 하는 model parameter $\theta$ 을 찾는 것을 목표로 합니다. 통계학적인 용어로 이를 Maximum Likelihood Estimation (MLE)라고 합니다. MLE는 데이터 관점에서 추정하는 방법인데, 쉽게 설명하면 “주어진 dataset $\mathcal{D}$가 관측될 확률 $p(\mathcal{D} \mid \theta)$ 를 최대화 할 수 있는 $\theta$를 추정하자” 라는 의미입니다. 이 MLE를 수식으로 표현하면 다음과 같습니다:
\[\begin{equation} \theta_{\text{MLE}} = \arg\max_{\theta} p(\mathcal{D} \mid \theta) \end{equation}\]이 수식은 아마 대부분 아실거라 생각하는데, 저희가 보통 나타내는 Loss Function입니다. 즉, 위 MLE를 $-$를 붙여서 minimization 문제로 치환하면 저희가 보통 사용하는 Loss Function $\mathcal{L}(\theta)$입니다.
(다시 본론으로 들어와서) 하지만, MLE가 제일 보편적이긴 하지만 단점이 있습니다. 바로 관측된 데이터셋 $\mathcal{D}$에 전적으로 의존한다는 점입니다. 예를 들어 설명해 보겠습니다. 우리가 특정 dataset $\mathcal{D}_1$ 에 대해 최적의 $\theta^\ast$로 찾았다고 해봅시다. 이 $\theta^\ast$는 $\mathcal{D}_1$에서 최적일지라고, 데이터 분포가 조금이라도 다른 새로운 $\mathcal{D}_2$에 대해서는 최적의 해가 아닐 수 있습니다. 즉, 주어진 데이터가 너무 적거나 편향되어 있을 때, MLE는 그 데이터의 특성(심지어 노이즈까지)에 과도하게 맞춰 학습하려 할 것이고, 이것이 우리가 흔히 말하는 overfitting의 근본적인 원인이 됩니다.
그렇다면 overfitting을 방지하기 위해 $\mathcal{D}$를 보기 전에 $\theta$에 대한 사전(prior)에 가정을 하고 들어가면 어떨까요? 다시 말해, $\mathcal{D}$만을 보고 학습을 진행한다면 해당 data distribution에서 너무 벗어났을 때문제가 생길 수 있으니 $\mathcal{D}$을 보기 전 우리가 최적으로 찾을 $\theta$에 대해서 사전에 정의를 하고 들어가면 어떨까?라는 의미입니다. 이제 여기서 bayesian 관점으로 보게 됩니다. 즉, $\mathcal{D}$를 보기 전 $\theta$에 대한 prior를 고려하게 되고, 이를 Maximum A Posteriori (MAP) 추정이라고 합니다. 이를 수식으로 표현하면 다음과 같습니다:
\[\begin{equation} \theta_{\text{MAP}} = \arg\max_\theta p(\theta \mid \mathcal{D}) \end{equation}\]여기서 $p(\theta \mid \mathcal{D})$는 bayes 정리에 의해서 다음과 같이 전개할 수 있습니다:
\[\begin{equation} \theta_{\text{MAP}} = \arg\max_\theta \frac{p(\mathcal{D} \mid \theta) p (\theta)}{p(\mathcal{D})} \end{equation}\]위 식은 $p(\mathcal{D}\mid \theta)$ (Likelihood) 와 $p(\theta)$ (Prior)의 곱을 최대화하는 문제로 바뀝니다. 그리고 여기서 $p(\mathcal{D})$는 이미 알고 있는 상수로 취급할 수 있기 때문에 굳이 고려할 필요가 없습니다. 이제 그렇다면, 과연 $p(\theta)$를 어떻게 prior로 취급해서 문제를 풀 수 있을까요?
Prior Knowledge: Gaussian Prior $\mathbf{\theta}$
이제 앞서 언급한 gaussian prior에 대한 가정을 적용해 보겠습니다. $p(\theta)$를 확률분포로 표현할 수 있고, 이때 제일 standard한 $\mathcal{N}(0, \sigma^2)$를 따른다고 가정했을 때, $\theta$는 다음과 같이 관계식으로 표현할 수 있습니다:
\[\begin{equation} \theta \sim \mathcal{N}(0, \sigma^2I) \;\; \Rightarrow \;\; p(\theta) \propto \exp(-\frac{\|\theta\|_2}{2\sigma^2}) \label{eq:prior_gaussian} \end{equation}\]이 가정을 MAP 식에 대입해 보겠습니다. 곱셈 형태의 계산을 단순화하기 위해 양변에 Log를 취하고, 다시 음수(-)를 붙여 Minimization 문제로 치환하면 다음과 같습니다:
\[\begin{aligned} \theta_{MAP} &= \arg\min_\theta \left[ -\log p(\mathcal{D}|\theta) - \log p(\theta) \right] \\ &= \arg\min_\theta \left[ \underbrace{\mathcal{L}(\theta)}_{=\text{MLE}} - \log \left( \exp\left( -\frac{||\theta||^2}{2\sigma^2} \right) \right) \right] \end{aligned}\]위 식의 정리하면 $\log$와 $\exp$가 사라지면서 다음과 같이 나타낼 수 있습니다:
\[\begin{equation} \mathcal{L}= \textcolor{red}{\underbrace{\mathcal{L}(\theta)}_{=\text{MLE}}} + \textcolor{blue}{\underbrace{\frac{1}{2\sigma^2} ||\theta||^2}_{\text{Prior}}} \label{eq:map_min} \end{equation}\]이 식을 보면 위에서 정리한 WD Eq.\eqref{eq:weight_decay} 과 굉장히 유사합니다. 여기서 Eq.\eqref{eq:weight_decay}에서의 $\frac{\lambda}{2}$와 Eq.\eqref{eq:map_min}에서의 $\frac{1}{2\sigma^2}$만 다를 뿐, 형태는 완전히 똑같습니다. 즉, $\lambda = \frac{1}{\sigma^2}$ 면 완벽히 동치라 할 수 있습니다.
WD Ratio $\lambda$의 의미
우리가 관습적으로 사용하던 WD는 단순한 technique이 아닌 weight parameter가 $\mathcal{N}(0, \sigma^2I)$를 따르는 Prior (Eq. $\eqref{eq:prior_gaussian}$) 라는 concept을 가지고 접근한 방법이였습니다.
더 나아가, 여기서 $\lambda$와 분산 $\sigma^2$이 반비례 관계라는 점이 중요합니다. 보통 $\lambda$를 너무 크게 줬을 때 학습이 수렴하지 않는 경우가 생기곤 합니다. 또, $\lambda$를 너무 작게 줬을 때 WD의 온전한 효과를 보지 못하게 됩니다. 이런 case들을 분산 $\sigma^2$와 엮어서 생각하면 왜 그런지를 좀 더 잘 이해할 수 있습니다:
- $\lambda \uparrow$ $\Rightarrow$ $\sigma^2 \downarrow$ : Prior Distribution의 분산이 작다는 것은 variable들이 0으로 많이 몰리게 됩니다. 이럴 경우 dataset $\mathcal{D}$의 분포가 컸을 때, 최적의 $\theta$를 찾기가 어려움
- $\lambda \downarrow$ $\Rightarrow$ $\sigma^2 \uparrow$ : Prior Distribution의 분산이 크다는 것은 variable들이 비교적 잘 퍼져있다는 의미가 됩니다. 따라서 이 경우는 사실상 prior의 가정이 거의 들어가지 않게 되는 것과 비슷한 효과를 가지기 때문에 overfitting의 위험이 여전히 있습니다.
이러한 Prior($\lambda$)의 역할을 이해하면, 최근 딥러닝 모델들의 학습 설정, 특히 Vision Transformer (ViT)와 같은 최신 모델에서 왜 그토록 강한 WD를 사용하는지 명확히 이해할 수 있습니다.
일반적으로 Vision Transformer(ViT)를 ImageNet과 같은 datasets을 학습시킬 때에도, 기존 CNN 모델보다 훨씬 높은 $\lambda$ 값을 설정하곤 합니다. 이는 ViT가 가진 특성, 즉 model이 가진 ‘자유도’를 제어하기 위해서입니다. ViT는 학습 시 CNN과 달리 image의 pixel끼리의 연결성 또는 지역적 특성(Spatial Locality) 같은 제약 조건(Inductive Bias)가 거의 없습니다. 다시 말해, Weight Parameter가 최적의 해를 찾기 위해 탐색해야 할 공간(Hypothesis Space)이 매우 넓다는 것을 의미합니다.
이렇게 학습 시 weight가 탐색할 space 자유도가 높을 때 데이터가 무한히 많다면 장점이 되지만, 데이터가 제한적일 때는 단점이 되곤 합니다. 데이터의 사소한 noise까지 학습해버려 overfitting이 발생하기 쉽기 때문입니다. 만약 이때, WD를 통해 model parameter에 Prior라는 제약(Condition)을 걸어줄 경우, weight이 탐색해야 할 유효 공간이 훨씬 좁아지게 되고, 결과적으로 Overfitting을 효과적으로 방지할 수 있게 됩니다.
이 예시와 앞서 전개한 수식들을 종합해 볼 때, 결론은 다음과 같습니다. 결론적으로 WD는 단순한 regularizer의 역할로써만 바라볼 것이 아니라 데이터에 전적으로 의존하는 학습(MLE)에, 우리가 가정한 사전 분포(Given Prior / Gaussian Distribution Assumption)를 반영하여 최적의 해를 찾아가는 균형 잡힌 과정이라고 할 수 있겠습니다.
2) LLM에서의 WD
위에 내용은 WD와 overfitting간의 연결성을 보였습니다. 그런데 사실 WD는 overfitting을 방지하기 위해서만 사용하진 않습니다. 예를 들어, 위에서도 살짝 언급했지만 overfitting을 고려하지 않아도 되는 Large Language Model (LLM) 학습에서도 WD를 강하게 걸어줍니다. 그 이유에 대해서 한번 보겠습니다. 여기서는 다시 딥러닝 학습을 optimization 관점으로 바라보겠습니다.
(해당 내용은 Stanford CS336 LLM from Scratch의 Lecture 3의 내용을 일부 발췌했습니다.)
LLM Only Trains Once
우선 LLM의 학습 특성을 이해할 필요가 있습니다. GPT-3, LLaMA와 같은 LLM의 목표는 특정 Task가 아닌 다양한 Task를 수행하는 Generalist가 되는 것이며, 이를 위해 인터넷 전체를 크롤링했다고 해도 과언이 아닐 만큼 방대한 데이터를 학습합니다.
데이터가 워낙 방대하다 보니, LLM은 1 Epoch만 학습하는 것이 일반적입니다. 같은 데이터를 반복해서 보지 않고 한 번만 훑고 지나간다는 뜻입니다. 이 관점에서 볼 때, 전통적인 의미의 overfitting은 LLM에서 고려할 사항이 아니긴 합니다. 그럼에도 불구하고, 왜 LLM은 WD를 강하게 걸까요?
LLM Needs More Gradients
그 이유는 Learning Rate (LR) Scheduling과의 상호작용에 있습니다. 최근 LLM 학습은 대부분 Cosine Decay와 같은 스케줄링을 사용합니다. 학습 초반에는 Warm-up을 통해 LR을 높였다가, 학습이 진행될수록 서서히 줄여나가 막판에는 0에 가깝게 만드는 방식입니다.
문제는 학습 후반부입니다. LR이 매우 작아지면, weight를 업데이트하는 보폭(Step Size)이 줄어들 뿐만 아니라 gradient 자체의 영향력도 미미해집니다. 즉, model이 더 이상 유의미한 학습을 하지 못하고 정체될 위험이 있습니다.
바로 이 관점에서 loss term에 포함된 WD의 역할이 중요해집니다. 이에 대해 아주 명확히 규명된 것은 아니지만, 최근 연구/논문들을 통해 실험적으로 밝혀진 현상이 있는데, 아래 Figure 1을 통해 그 결과를 확인할 수 있습니다. Figure 1을 자세히 보면, WD를 강하게 주었을 때 학습 초반부의 Training Loss 값은 다소 클지라도, 최종적으로는 WD를 더 크게 준 경우의 Training Loss 값이 더 낮게 수렴하는 것을 확인할 수 있습니다.

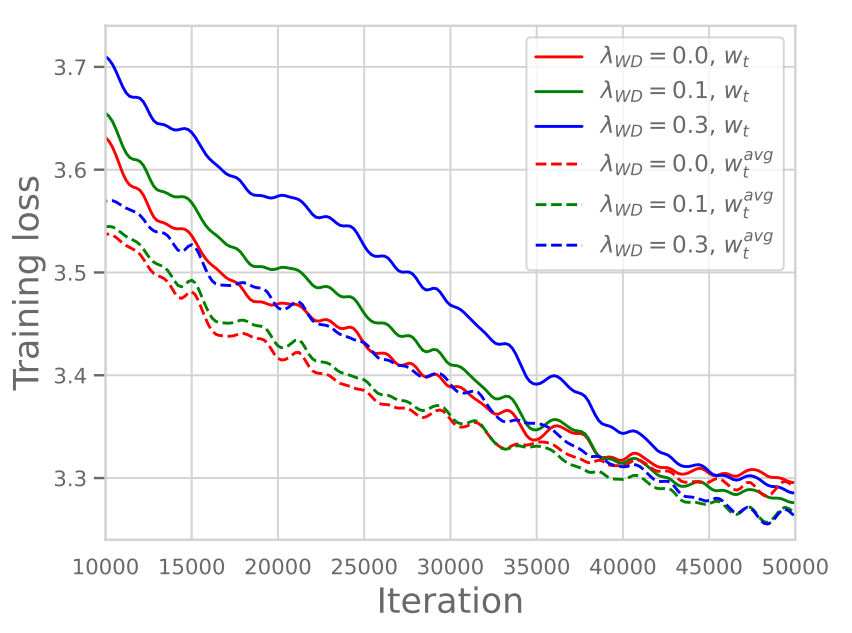
해당 강의에서 Hashimoto 교수는 이를 다음과 같이 해석합니다.
(의역)LR Scheduling으로 인해 학습 후반부로 갈수록 Learning Rate은 줄어들게 되고, 이에 따라 Gradient 또한 줄어들어 학습 막판에는 학습 효과가 미미해질 수 있습니다. 이때 WD를 강하게 걸어주면, 학습 막판에도 Gradient 값들을 어느 정도 크기로 유지시켜 주어 지속적인 학습을 가능하게 한다는 것입니다.
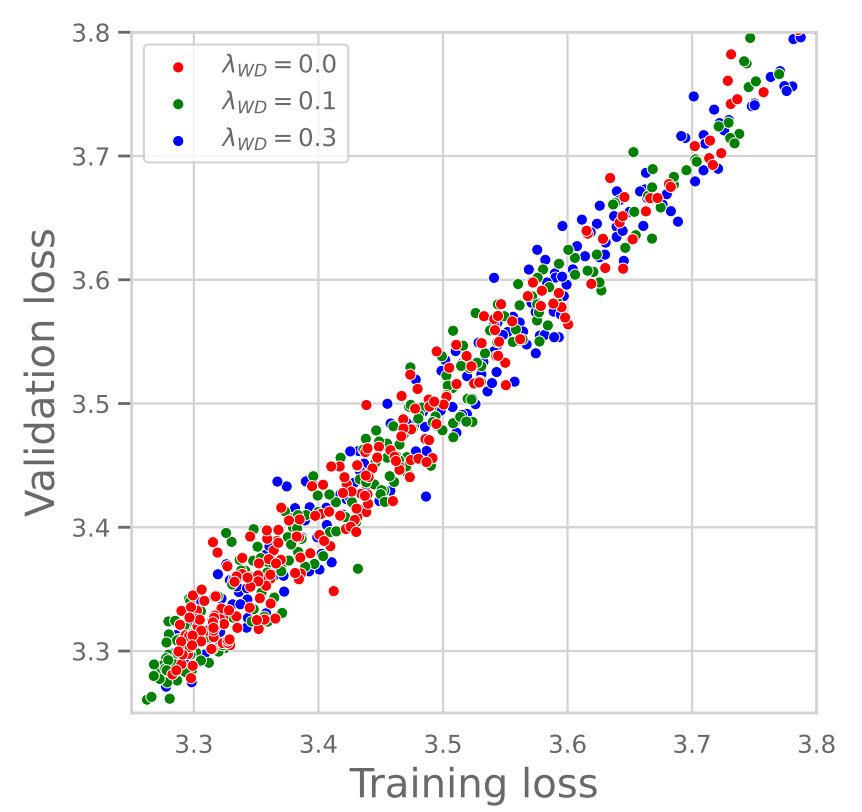
이를 뒷받침하는 연구 결과도 해당 논문에 아래 Figure 2와 같이 나와있습니다.
우선 왼쪽 그래프를 보시면 WD 값에 따른 Training & Validation Loss 간의 관계를 나타내고 있습니다. 그래프에서 볼 수 있듯이, WD 값이 크든 작든 Training Loss와 Validation Loss 값이 거의 동일하게 나타납니다. 즉, WD 크기에 상관없이 Generalization Gap이 거의 0에 수렴한다는 것을 알 수 있습니다. 이는 LLM 학습에서 WD가 Overfitting 방지(Generalization)와는 관련이 없음을 명확히 보여줍니다.
반면, 오른쪽 그래프는 Constant LR(Learning Rate를 줄이지 않고 일정하게 유지)일 때의 WD에 따른 결과를 보여줍니다. 여기서는 Figure 1과 다르게, WD가 클수록 오히려 Training Loss 값이 커지는 것을 확인할 수 있습니다. 즉, LR이 줄어들지 않는 상황에서는 WD를 강하게 거는 것이 단순히 Prior를 강하게 제약하는 효과로만 작용하여 오히려 성능에 손해를 끼친다는 점을 확인할 수 있습니다.
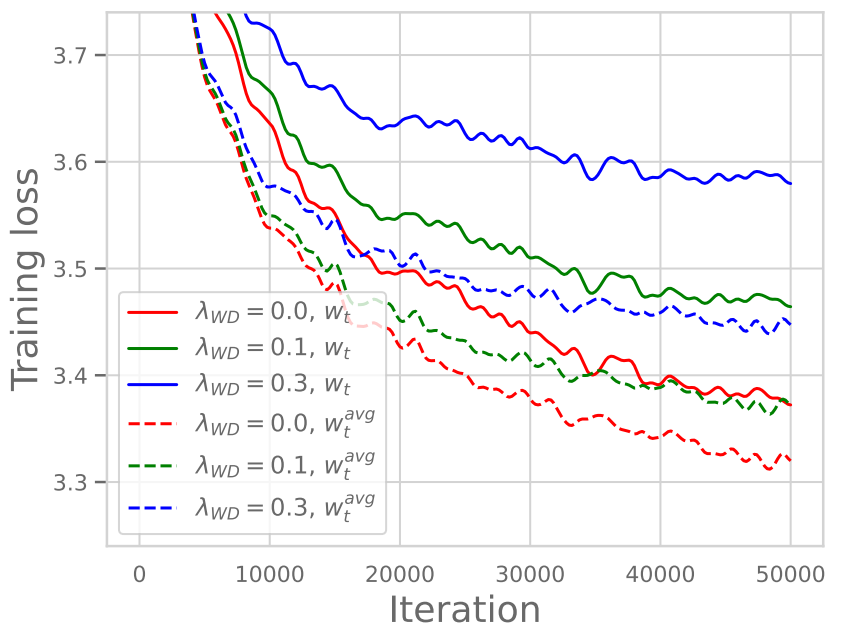
위 내용들을 종합해 봤을 때, LLM에서의 WD는 기존 overfitting 방지하는 개념과 달리, LR Scheduling과 결부되어 학습의 지속성을 유지하기 위해 사용된다고 이해하면 좋을 것 같습니다.
결론
결론적으로 Weight Decay (WD)는 두가지 관점으로 볼 수 있는데, 통계적 관점(Statistical Perspective), 그리고 최적화 관점(Optimization Perspective)으로 볼 수 있을 것 같습니다:
통계적 관점(Statistical Perspective)에서 볼 때, 데이터에 전적으로 의존하는 MLE 방식에 Gaussian Prior를 도입하여 MAP 추정으로 전환함으로써, 데이터의 편향을 막고 안정적인 해를 찾게 해줍니다.- 동시에
최적화 관점(Optimization Perspective)에서는, LLM과 같은 대규모 학습 시 Learning Rate Decay가 진행됨에 따라 줄어드는 Gradient의 크기를 보존하여 학습의 지속성을 보장하는 역할을 수행합니다.
즉, WD는 setting에 따라 통계적 관점의 최적의 해를 탐색하기 위해 Prior를 통한 탐색 공간(Hypothesis Space) 제한과 최적화 관점의 학습 동력 유지 라는 두 가지 핵심 기능을 수행한다고 정의할 수 있을 것 같습니다.
모처럼 딥러닝에서 사용되는 개념에 대해서 정리를 해봤습니다. 가끔씩 자주 사용하지만 그 beyond까지 살펴볼 수 있는 개념 관련해서도 종종 포스팅 하도록 하겠습니다. 읽어주셔서 감사합니다!!